Le Paraboloïde hyperbolique

Le Paraboloïde hyperbolique

ou

 l’ardente recherche de l’inutile

« Que nul n’entre ici s’il n’est géomètre » disait Platon de son Académie. Heureusement, Platon était au moins autant poète que géomètre, et il n’est pas le seul. Mais Jean-François Dalloz fait pressentir que la vision géométrique et le vocabulaire même de cet art qu’il aime passionnément peuvent être poétiques, et que le poète est un visionnaire… que l’enthousiasme aveugle.

J’ai coulé des jours heureux à Champollion. De surcroît j’ai eu le plaisir d’avoir en math les plus grands professeurs, qui suscitèrent en moi un amour immodéré pour la géométrie, M. Roux, expert en géométrie cotée, M. Miellou, géomètre dans l’âme. Dans le secondaire, je passais de l’un à l’autre, et leurs fameux manuels régnaient alors sur l’univers des lycées. En prépa, M. Bruce nous initiait à la géométrie analytique avec sa kyrielle de courbes paramétrées : astroïdes, conchoïdes, strophoïdes, cardioïdes, lemniscates, courbes enveloppes. Quant à M. Bernard, il ne jurait que par les quadriques et les biquadratiques.

On lui doit le fameux théorème selon lequel le plan osculateur en un point M d’une biquadratique Q n’est autre que le plan tangent en M au paraboloïde hyperbolique passant par Q. Je me souviens d’une épure où une sphère et un paraboloïde de révolution étant bitangents à l’infini suivant le cône isotrope, leur intersection se réduisait à un cercle. (Les médecins, les philosophes et les informaticiens ne sont pas les seuls à avoir un langage peu accessible au commun des mortels).

La vie professionnelle consacrée, en ce qui me concerne, à la construction de bateaux, m’éloigna de ces sujets passionnants. La technique, les délais et les coûts étaient devenus mon pain quotidien. Choyer le client sans se brouiller ni avec les fournisseurs ni avec mes collègues me donna un tempérament d’équilibriste si bien que mes préoccupations mathématiques se rapprochèrent assez vite de la “ théorie des catastrophes ” chère à René Thom. Je frisais la méningite aiguë en lisant Les Origines de la Géométrie de Michel Serres, et finalement je perdais de vue la géométrie en courant droit à la catastrophe, comme on va bientôt le voir.

Au fil des années la construction navale devint une industrie de plus en plus assistée et en 86, Normed, qui regroupait les chantiers navals de Dunkerque, La Seyne et La Ciotat, fit faillite. Faillite inéluctable, les pouvoirs publics (de droite puis de gauche) refusant de proroger l’aide massive qui avait permis de garder Normed la tête hors de l’eau. J’ai eu la chance de terminer les contrats en cours à La Ciotat puis de bénéficier de l’active solidarité de mes concitoyens en attendant que vienne la retraite.

C’était donc l’occasion que m’offrait la Providence pour revenir à la géométrie.

Parlons tout d’abord de paraboloïde hyperbolique (PH). Comme le montre la figure 1, c’est une surface réglée. Un plan tangent en M le coupe suivant deux droites (génératrices G) concourantes en M. Tout autre plan le coupe selon une hyperbole H ou une parabole P, d’où son nom. Forme qui s’apparente à une selle de cheval, difficile à réaliser, et de ce fait peu courante en architecture, malgré son indéniable esthétique. Je l’ai rencontrée trois fois : le toit de la piscine de Saint-Auban (Alpes de Haute-Provence), le toit de l’église de Davos (Suisse), un treillis dans un jardin zoologique de Mexico (Mexique). Persuadé que cette forme avait un grand avenir devant elle, j’imaginais des barres constituées par juxtapositions de facettes en forme de pa­raboloïde hy­perbolique. La barre “ hy­perbo ” (fi­gure 2) était née.

Le pre­mier hy­per­bo était en papier dé­coupé et collé. Le département génie mécanique de l’IUT de Toulon à qui je montrais cette maquette s’intéressa à la chose. Des “ barres ” en aluminium furent réalisées par une fraise à tête sphérique pilotée par une machine à commande numérique à trois mouvements simultanés commandés par ordinateur. La sphère de la fraise réalisait l’usinage en suivant les génératrices rectilignes tout en restant tangente à la surface du PH. J’ai passé tout un dimanche à calculer la trajectoire du centre de la sphère qui ressemble à une hélice à pas variable.

Chaque “ face ” d’hyperbo est délimitée par quatre génératrices égales, deux génératrices ayant une extrémité commune faisant entre elles un angle de 70,5° ¹. Toutes les faces de l’hyperbo sont identiques. De ce fait les barres hyperbo peuvent s’assembler entre elles suivant deux directions perpendiculaires ou trois directions trirec­tangulaires (Figures 3, 4 et 5).

Pressentant que ce principe d’assemblage était applicable dans le bâtiment (murs, piliers, voûtes, linteaux, ossatures en tous genres), je consulte le CSTB (Centre scientifique et technique du bâtiment) où je reçois de chaleureux encouragements. Je contacte différents syndicats de constructeurs (blocs de bé­ton, produits céramiques, béton cellu­laire…). Je sollicite l’AN­VAR en vue d’ob­tenir le fi­nancement du “ diag­nostic inno­vation ” du CSTB. Je fais des recherches d’antériorité et dépose un brevet en 87, que l’INPI (Institut national de la propriété industrielle) entérine un an plus tard. Ma demande ayant  été acceptée par l’ANVAR, je nage dans l’euphorie et je prépare le dossier du diagnostic innovation. C’est ici que se situe la frontière entre “ l’ardente recherche ” et “ l’inutile ”.

 Je prends du retard dans la préparation du dossier, et de ce fait l’ANVAR refuse la sub­vention, qui a été déprogrammée de son budget. Entre temps, le CSTB qui a examiné de plus près mes proposition m’accroche à juste titre sur les problèmes d’étanchéité. L’hyperbo, dont l’avantage potentiel était de réduire massivement les frais de main d’œuvre grâce à son aptitude au montage à sec, devient alors inapte à la construction des bâtiments.

Je m’obstine. Je fabrique deux moules avec lesquels je réalise un petit millier de barres en plâtre que je colle entre elles, cherchant inlas­sablement la combi­naison qui me permettrait d’utiliser au mieux les possibilités de ce “ pavé autobloquant tridirectionnel ”. Peine perdue, il n’y a rien à en tirer. La seule application possible s’avère être le jouet, les enfants passant des heures à assembler les barres. Mais le marché est nettement insuffisant, et j’ai donc finalement jeté l’éponge, ni malheureux, ni déçu. Le brevet est maintenant dans le domaine public, à la disposition de tous ceux qui voudraient s’a­donner à l’inutile avec passion.

 
Mais toi, lec­teur avisé, qui as eu la patience de me lire jusqu’au bout, sois assez bon maintenant pour arracher ces pages qui n’ont pas leur place dans notre illustre Cambuse. Mets-les dans une bouteille que tu jetteras à la mer. Peut-être arriveront-elles un jour sur un rivage où depuis toujours on rêve de paraboloïdes hyperboliques.

Les schémas suivants éclairent l’utilisation réelle des hyperbos.

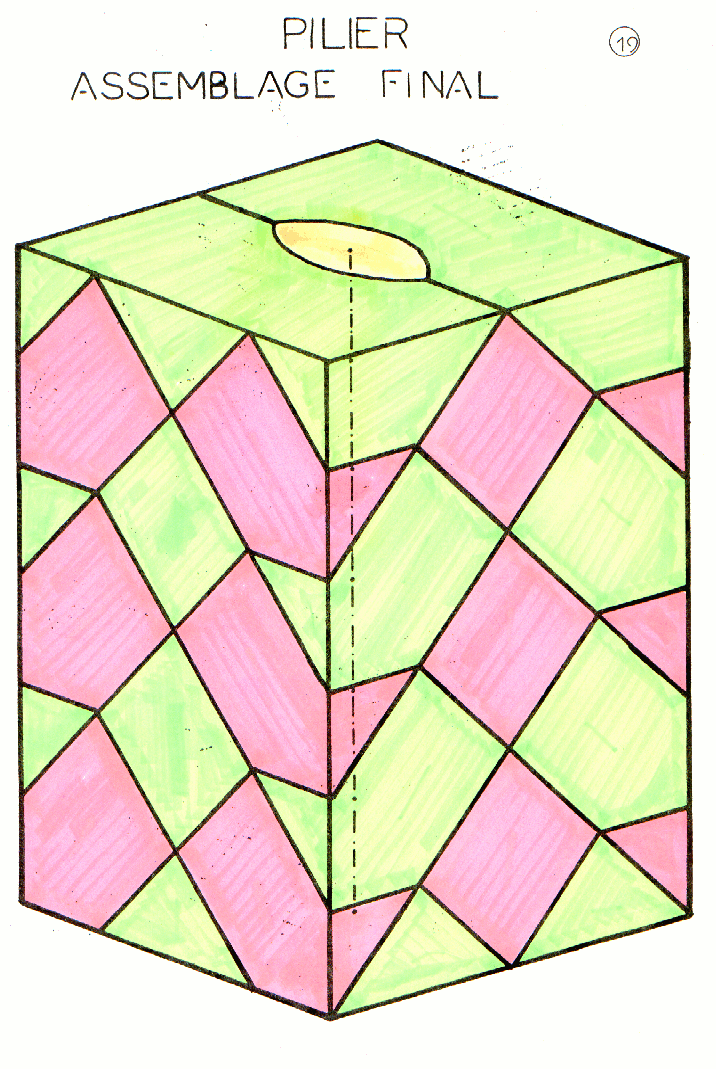
Jean-François Dalloz (La Seyne-sur-Mer - 83)